珍しい苗字の五郎丸さんの功労もありラグビーがちょっとしたブームで
なおかつ私の好きなNFL(米国アメリカンフットボールリーグ)も始まり
長細いボールを見る機会が増えましたが、
あれを「楕円球、楕円ボール」と呼ぶのは実は間違いなのです。
「楕円」(だえん、橢円とも。ellipse)とは、平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線で
2次元直交座標系で、原点 O が長軸と短軸の交点となる楕円は代数的に次のように書ける。これを標準形という。
a > b > 0 のとき、2a は長軸の長さ(長径)、2b は短軸の長さ(短径)となる。xy 平面上にグラフを書くと横長の楕円となる。また、焦点はx 軸上にあり、その座標は 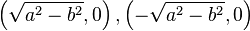 となる。
となる。
b > a > 0 のときは逆に、2b が長軸の長さ(長径)、2a が短軸の長さ(短径)となる。したがって、xy 平面上にグラフを書くと縦長の楕円となる。また、焦点は y 軸上にあり、その座標は  となる。
となる。
同じ楕円は、t を媒介変数とする媒介変数表示では、次のように表現できる。
ただし、t は楕円の偏角を意味していない( 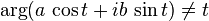 である。)。
である。)。
楕円の形状は離心率 e で表現される。
別途、扁平率 f でも表現できる。
楕円の面積 S は次のように表現できる。
楕円の周長 C は a > b のとき、第二種完全楕円積分を用いて次のように表現できる。
また 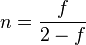 とおき、二項係数を使って、次のようにも表現できる(Gauss-Kummer級数)[1]。
とおき、二項係数を使って、次のようにも表現できる(Gauss-Kummer級数)[1]。
計算機で計算する場合に有用な式としては、分母が  の率で消える式が次のように導出されている[2]。
の率で消える式が次のように導出されている[2]。
近似式としては、シュリニヴァーサ・ラマヌジャンによる次の二式がある。簡便なものとしては、
があり、さらに良い近似として、次式がある。
より一般的には、対応する角度の関数としての、周長の一部である楕円弧長は、第二種不完全楕円積分で表される。
すでにおわかりのように、これらの定義から
ラグビーやアメリカンフットボールのボールは楕円ではないのです
これらのボールの形状は、「長球」と言われ
楕円をその長軸を回転軸として回転したときに得られる回転体で。長球は3径のうち短い2径の長さが等しい楕円体とも定義できる。言い換えれば、長球は短半径が赤道半径、長半径が極半径の回転楕円体である。
長球の表面積 Sはb > aの条件下で、

長球は、短半径aと長半径bからなる長軸の回転楕円体であり、離心率eと定義される。
これで明確におわかりいただけたかと思いますが
ラグビーやアメリカンフットボールのボールは
正確には「長球球」なのです
ね!勉強になりましたねぇ
(頭がウニのようになった、理科系の)
BAKUでした。

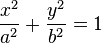
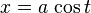
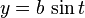




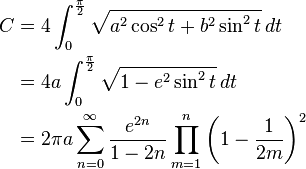



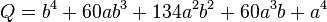


![C \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]= \pi \left[3(a+b)-\sqrt{10ab+3(a^2+b^2)}\right]](https://upload.wikimedia.org/math/9/8/f/98fe993c7427f52b03ef3a53a9d0b331.png)


 と表される。
と表される。